Processing 3D でクォータニオンを用いて回転する

 

とある都合でクォータニオン( Quaternion )で得た数値をProcessingで利用するためにいろいろ調べたのでメモがてら書きます．
簡単にクォータニオンの説明と，それをProcessingで使うためのTipsを書いています．

 

クォータニオン とは 四元数(wiki)のことです．
3Dプログラミングでは，クォータニオンを用いて回転を処理することが多いです．
回転と聞くとX軸回転，Y軸回転，Z軸回転のようなものを思い浮かべますが，これはオイラー角と呼ばれるものを利用した回転になります．
クォータニオンやオイラーは回転に用いられますが，とあるもとの状態を設定することで物体の姿勢を意味することもできます．

 

オイラー角を用いた回転は非常にシンプルで，どの軸基準で何度回転させるかというだけです．
以下の例でははBlenderを用いています．
 

 
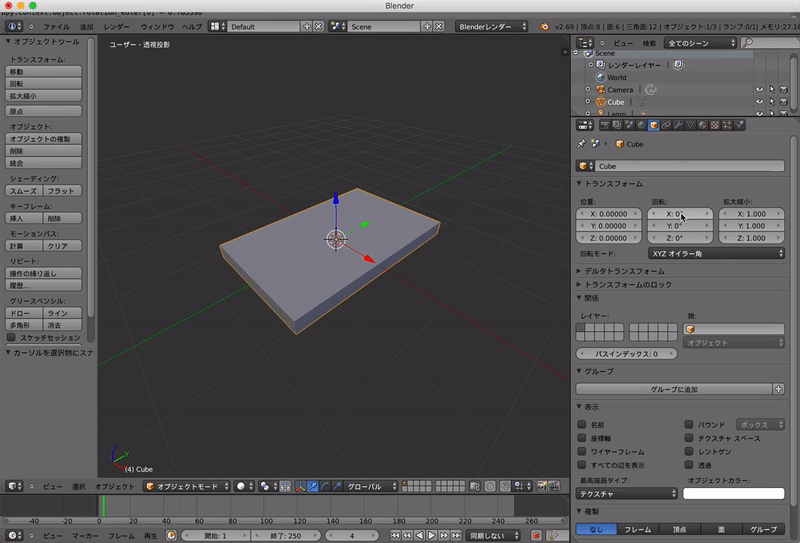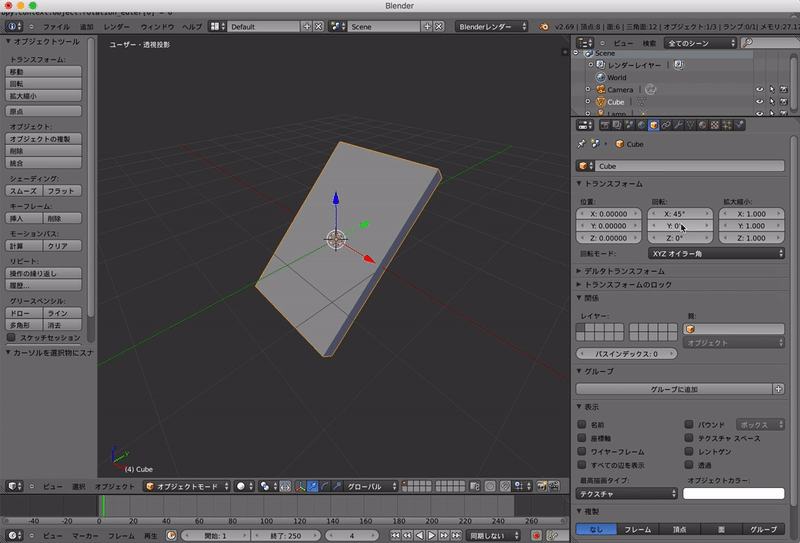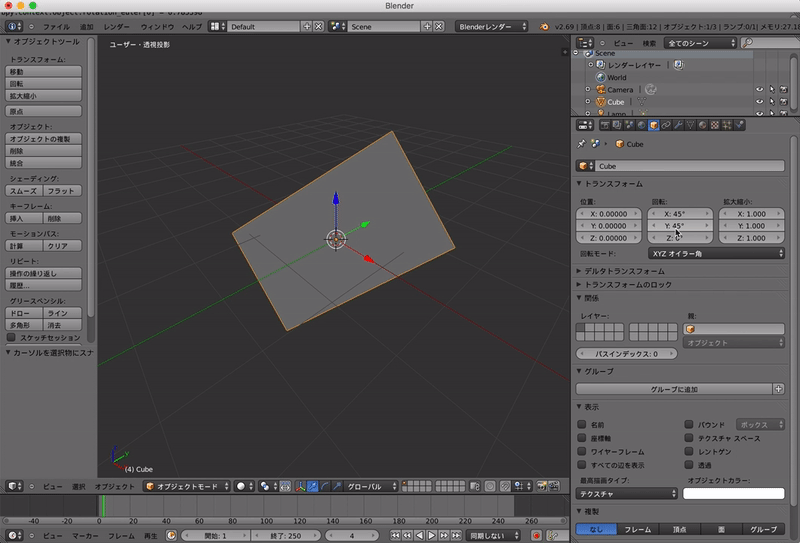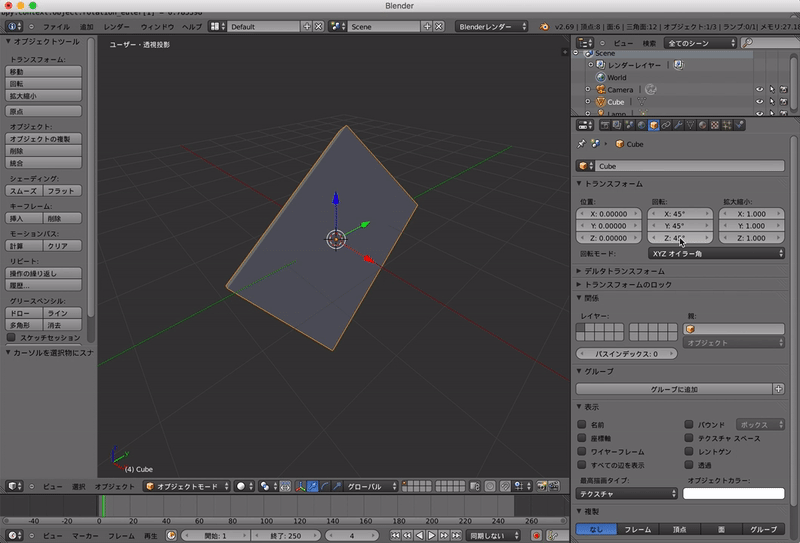
しかしオイラー角では回転する軸の順番で，向きが変わってしまいます．
Blenderでは「回転」の下に「XYZオイラー角」とあると思います．これはXYZの順番で上の角度ど回転した結果を意味します．
なので，以下のように「ZYXオイラー角」を用いると最終的な向きは変わってしまいます．
 

 

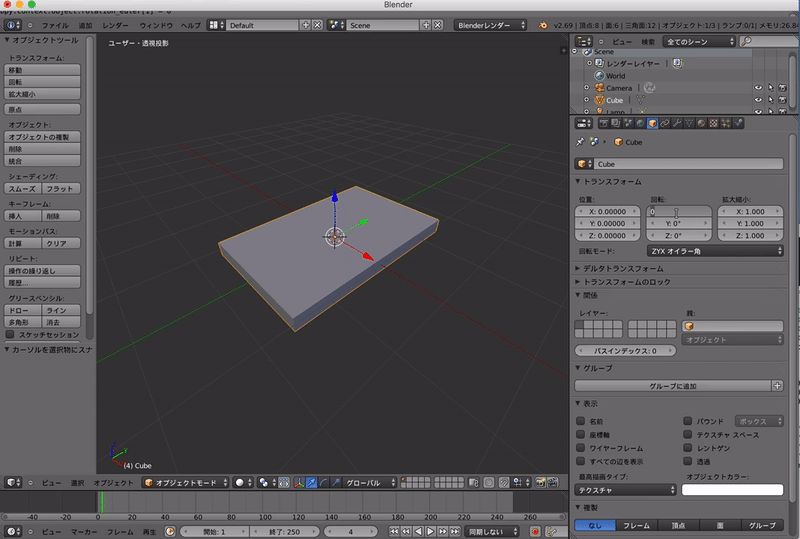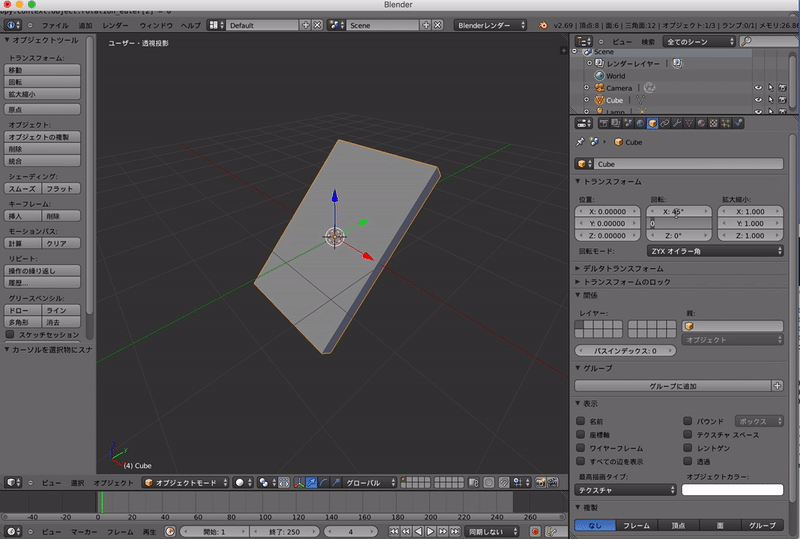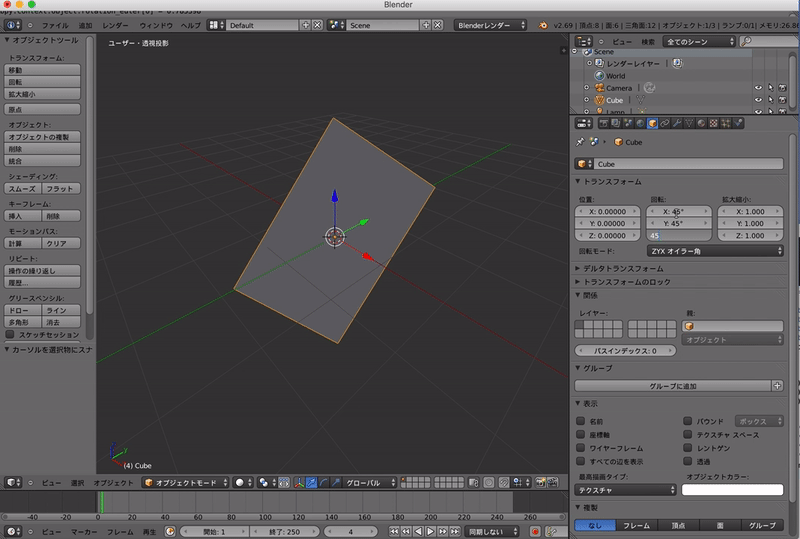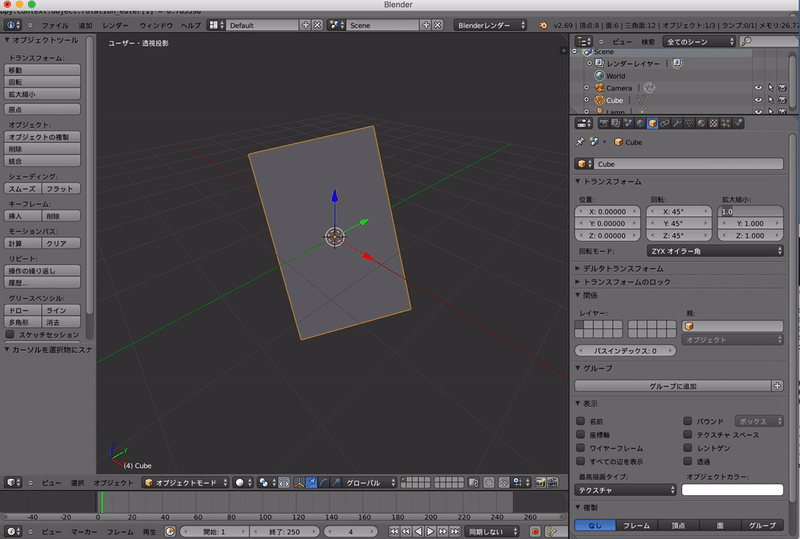
このようにオイラー角を使うとどのような角度にさえ回転できるとはいえ回転する順番で結果が変わってしまいます．

一方クォータニオンを使った回転は一発で決まります．

 

クォータニオンは次のように表記されます．
$$
Q = (w; V) \\
w = cos(θ/2) \\
V = (x,y,z) \\
x = αsin(θ/2), y = βsin(θ/2), z = γsin(θ/2)
$$

wは実部，Vは虚部のベクトルで，以下のように距離は１になります．
$$ \sqrt{α^2 + β^2 + γ^2} = 1$$

このベクトル軸まわりでθ回転するというイメージです．

 
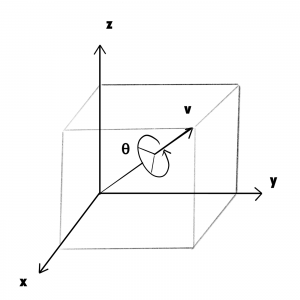
例えば，x軸とy軸の間の軸(以下の画像のv)で45度(π/4)回転してみましょう．

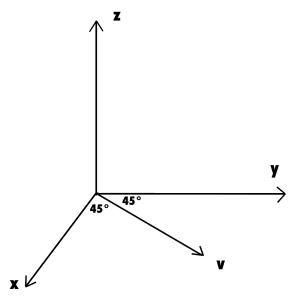
xとyの大きさが同じなので，γ=0, α=βとなります．
$$
\sqrt{α^2 + β^2 + γ^2} = 1 \\
α = β = \sqrt{0.5} = 0.70710678118 \\
$$
$$
(w; a, y, z)\\
= (cos(θ/2); α sin(θ/2), β sin(θ/2), γ sin(θ/2) ) \\
= (cos(π/8); \sqrt{0.5} sin(π/8), \sqrt{0.5} sin(π/8), 0 sin(π/8) ) \\
= (0.9238; 0.2705, 0.2705, 0)
$$
これも，Blenderを使って簡単にデモしてみます．

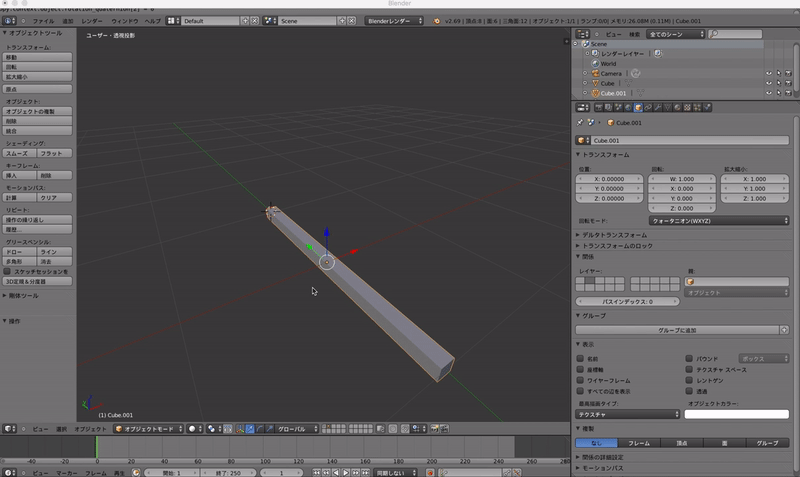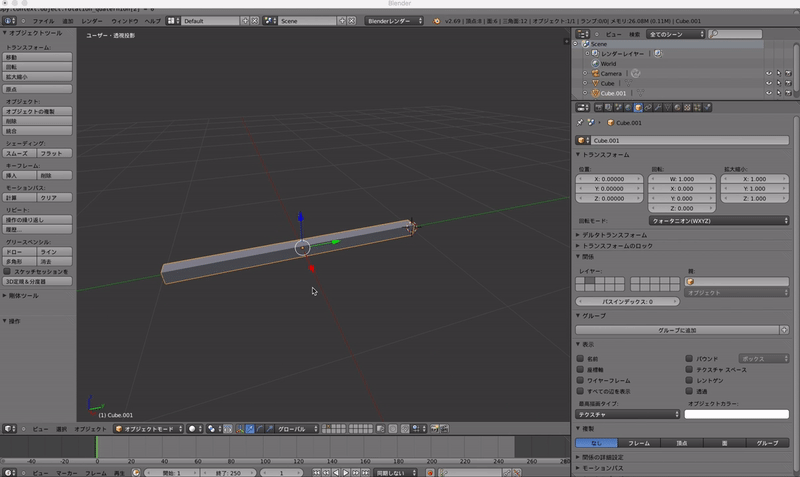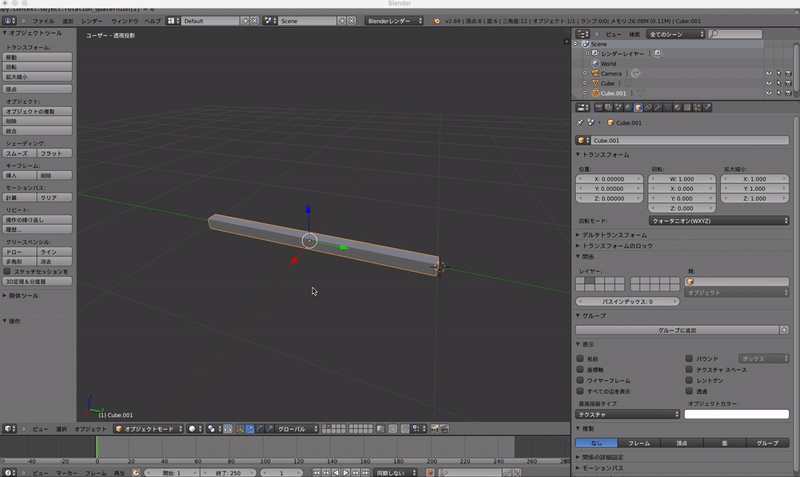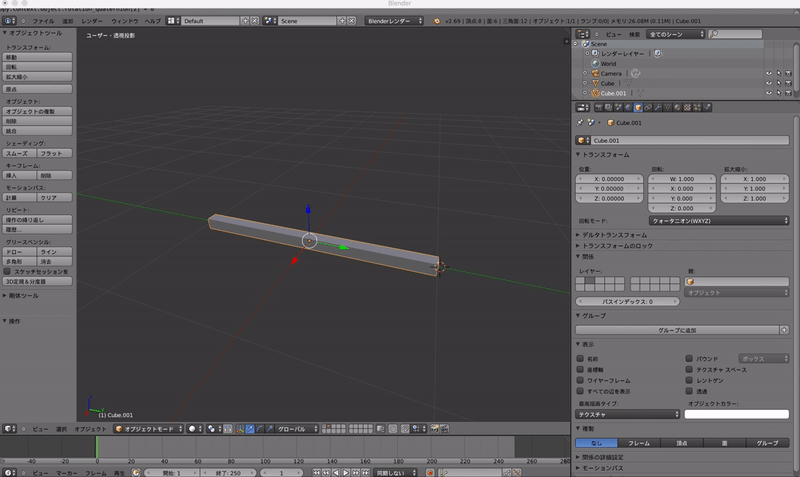
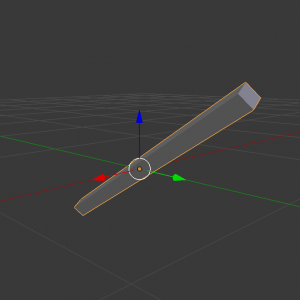
このように，y軸に長い棒を使ってみます．
これに上の数値を入れて回転してみましょう．
数値入れるとこがちょっと見にくいですが，右のウインドウで入力しています．

 

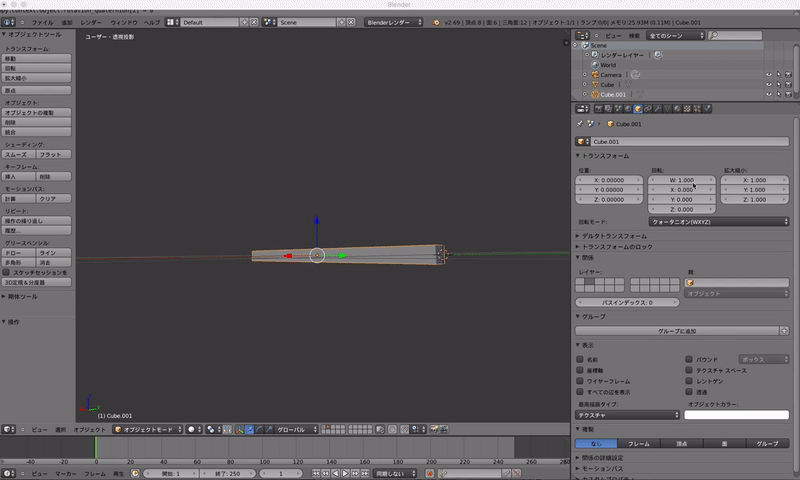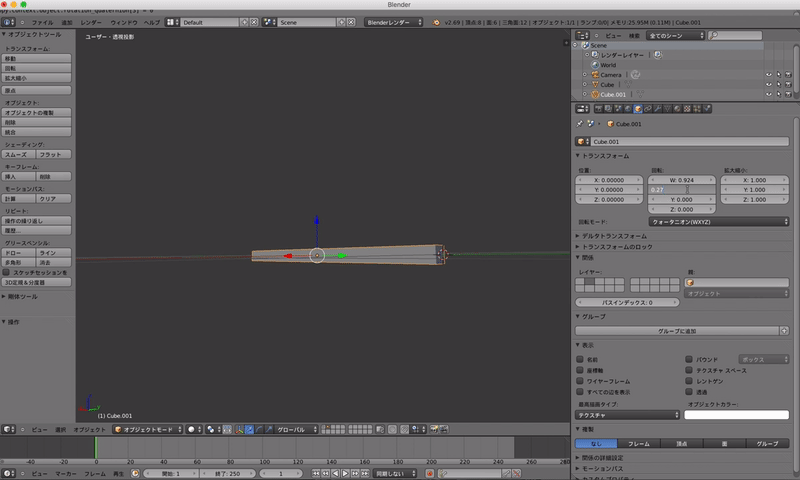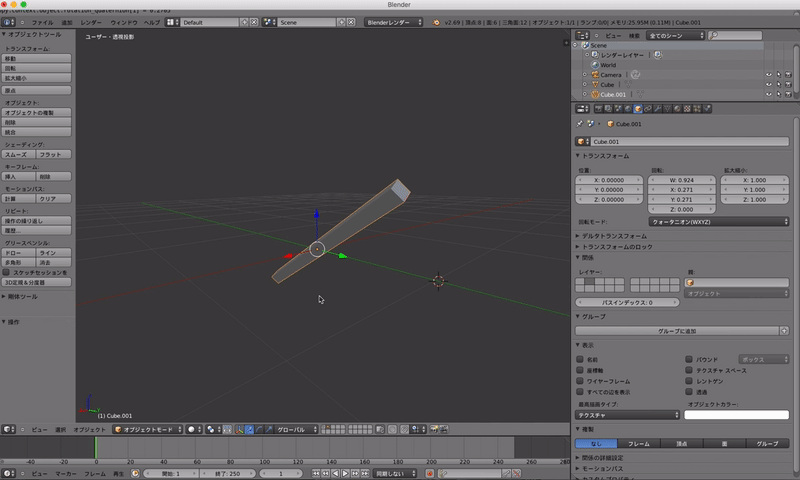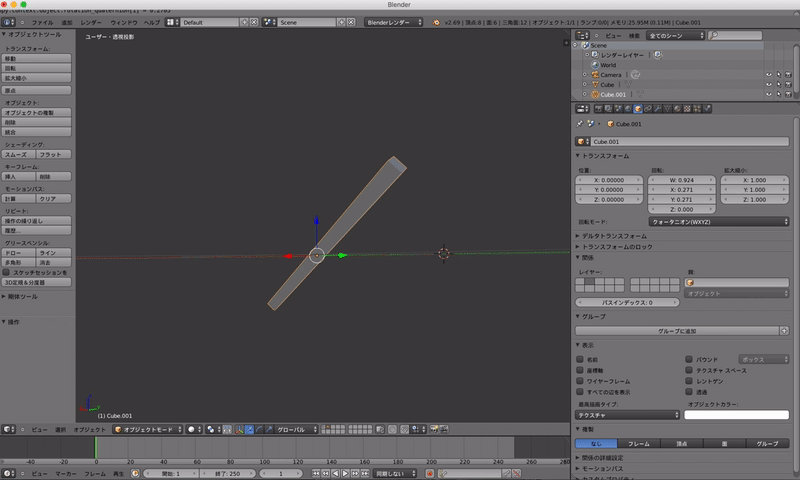
x軸とy軸の間の軸で45度回転してます．

 

Processing ではオイラー回転しかできないので，クォータニオンをオイラー角に変換する必要があります．

 

このソースはググったら出てきたので，それをProcessing(java)で書き換えて使います．

float[] quaternion_to_euler_angle(float x, float y, float z, float w) {
  float ysqr = y * y;

  float t0 = 2.0 * (w * x + y * z);
  float t1 = 1.0 - 2.0 * (x * x + ysqr);
  float X = atan2(t0, t1);
  
  float t2 = 2.0 * (w * y - z * x);
  t2 = (t2 > 1.0)? 1.0:t2;
  t2 = (t2 < -1.0)? -1.0:t2;
  float Y = asin(t2);
  
  float t3 = 2.0 * (w * z + x * y);
  float t4 = 1.0 - 2.0 * (ysqr + z * z);
  
  float Z = atan2(t3, t4);

  float[] forReturn = new float[3];
  forReturn[0] = X;
  forReturn[1] = Y;
  forReturn[2] = Z;
  return forReturn;
}

 

座標軸が同じ場合であればquaternion_to_euler_angleで得た数値をそのまま使えばよいです．
Blenderの座標は右手系(X:親，Y:人指, Z:中指)なのですが，Processingは左手系でZ軸の向きが逆になり，またX,Y軸の回転が逆になります．
なのでそのままの数値で回転すると，結果が変わってしまいます．

ここから先はどのように表示したいかによって対応が変わります．
例えば，Y軸の向きを反転してそれ以外は同様のまま表示したい場合は，

float [] euler = quaternion_to_euler_angle(quaX, -quaY, quaZ, quaW);
rotateX(-euler[0]);
rotateY(-euler[1]);
rotateZ(-euler[2]);

のように，y軸に関しては向きを反転させます．
回転が逆回転になっているのは，Processingではオブジェクトを回転するのではなく座標軸を回転させてから物体を置くという流れになっているからです．
すると以下のようにy軸に関しては反対の向きになりますがそれ以外はBlenderのときと同様に表示させることができます．

 

上の画像を生成するにあたって用いたソースコードです．
ぜひ色々いじってみると良いと思います．

import processing.opengl.*;

float quaX = 0;
float quaY = 0;
float quaZ = 0;
float quaW = 0;

int camX = 500;
int camY = 500;
int r = 500;
float draggedPreX = 0;
float theta = PI/4;
void setup() {
  size(500, 500, OPENGL);
    
  rectMode(CENTER);
}


void draw() {
  background(100);
  
  stroke(255,0,0);
  line(0, 0, 0, 300, 0, 0);
  stroke(0,255,0);
  line(0, 0, 0, 0, 300, 0);
  stroke(0,0,255);
  line(0, 0, 0, 0, 0, 300);
  stroke(0);
  
  camX = int(r * cos(theta));
  camY = int(r * sin(theta));

  camera(
    camX, camY, 500,
    0, 0, 0,
    0.0, 0.0, -1.0
  );

  quaX = 0.2705;
  quaY = 0.2705;
  quaZ = 0;
  quaW = 0.924;

  pushMatrix();
    float [] euler = quaternion_to_euler_angle(quaX, -quaY, quaZ, quaW);
    println( "euler : ", euler[0], euler[1], euler[2] );
    rotateX(-euler[0]);
    rotateY(-euler[1]);
    rotateZ(-euler[2]);
    box(20, 300, 20);
  popMatrix();

}


float[] quaternion_to_euler_angle(float x, float y, float z, float w) {
  float ysqr = y * y;

  float t0 = 2.0 * (w * x + y * z);
  float t1 = 1.0 - 2.0 * (x * x + ysqr);
  float X = atan2(t0, t1);
  
  float t2 = 2.0 * (w * y - z * x);
  t2 = (t2 > 1.0)? 1.0:t2;
  t2 = (t2 < -1.0)? -1.0:t2;
  float Y = asin(t2);
  
  float t3 = 2.0 * (w * z + x * y);
  float t4 = 1.0 - 2.0 * (ysqr + z * z);
  
  float Z = atan2(t3, t4);

  float[] forReturn = new float[3];
  forReturn[0] = X;
  forReturn[1] = Y;
  forReturn[2] = Z;
  return forReturn;
}

void mousePressed(){
  draggedPreX = mouseX;
}

void mouseDragged(){
  int x = mouseX;
  
  theta += (x-draggedPreX)/500;
  println(theta);
  draggedPreX = x;
}