マハラノビス距離 を用いたクラスタリング
マハラノビス距離( Mahalanobis ‘ Distance)とは主に統計で用いられる分散を考慮した距離の一種です。
詳しくはwikiで見てください。
今回はこのマハラノビス距離を用いた教師あり機械学習をpythonで実装します。
例として2次元の特徴を持つテストデータのクラスタリングを行っていますが、
実装としては(メモリが許す限り)N次元の特徴を持つ学習にも対応しています。
コードの全文はGithubにあげています。
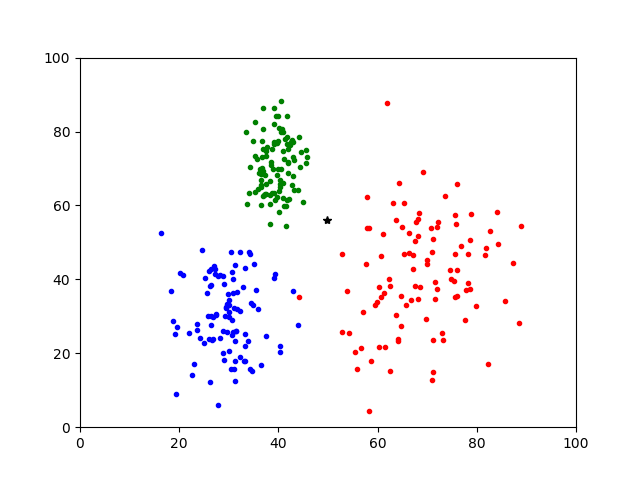
この画像の黒*点はどこに属するでしょうか。
各クラスの平均値との距離を取るだけではこの*点は緑のほうが近そうです。
しかし、赤は広く分布しているので、おそらくは赤でしょう。
マハラノビス距離を使えば、このように分散が異なるクラスに対してユークリッド距離を用いた手法より正確にクラスタリングできます。
マハラノビス距離の定義
マハラノビス距離を測るための準備として、学習データの平均値、分散、共分散を求めます。
K次元のデータ群に対し、クラスがcである
$$N^{(c)}$$
個の学習用データを
$$X^{(c)}_n = (X_{n1}, X_{n2},…, X_{nk})^T, n=1, …, N^{(c)}$$
とすると、各クラス毎に計算される平均ベクトルは
$$M^{(c)} = (M^{(c)}_1, M^{(c)}_2,…, M^{(c)}_k)^T $$
ただし,
$$ M^{(c)}_i = \frac{1}{N^{(c)}}\sum_{n=1}^{N^{(c)}} x_{ni} $$
と書け、
また、分散共分散行列は
$$
S^{(c)} = \left[
\begin{array}{rrrr}
S^{(c)}_{11} & S^{(c)}_{12} & … & S^{(c)}_{1K} \\
S^{(c)}_{21} & S^{(c)}_{22} & … & S^{(c)}_{2K} \\
… & … & … & … \\
S^{(c)}_{K1} & S^{(c)}_{K2} & … & S^{(c)}_{KK}
\end{array}
\right]
$$
ただし,
$$ S^{(c)}_{ij} = \frac{1}{N^{(c)}} \sum_{n=1}^{N^{(c)}} (x_{ni} – M^{(c)}_{i})(x_{nj}-M^{(c)}_{j}) $$
という式で書くことが出来ます。
そして、実際にテストデータと各クラスとのマハラノビス距離を求める式は以下のように書くことが出来ます。
$$ d^{(c)}_m(x)=(x-M^{(c)})^T(S^{(c)})^{-1}(x-M^{(c)}) $$
———
*2018/10/27追記
この式についてですが,次元kでさらに除する形の定義もあるそうです.
しかし,次元kは固定になるので相対的に結果の比は変わりません.
以下のコードではkで除していません.
———
この式から分かる通り、分散共分散行列Sの逆行列を利用しています。
なので、学習データが与えられた後にクラスごとの平均値とこの分散共分散行列の逆行列を求めます。
ちなみにユークリッド距離の式は
$$ d^{(c)}_e(x) = \sqrt{(x-M^{(c)})^T(x-M^{(c)})} $$
なので
分散共分散行列Sが単位行列Eのとき(S=Eのとき)
$$ d^{(c)}_m(x)=(d^{(c)}_e(x))^2 $$
となる関係があります。
マハラノビス距離の実装
少し複雑ですが、基本的に上の式にそのまま則ってるので、(pythonに慣れていれば)読めると思います。
xpと書かれていますが、numpy もしくは cupyで計算すると思ってください。
class mahalanobis:
def __init__(self, _trains, _targets):
print('# setup mahalanobis machine learning')
self.trains = xp.array(_trains, dtype=xp.float64)
self.targets = xp.array(_targets, dtype=xp.int32)
self.calc_convariance_matrix()
def calc_convariance_matrix(self):
print('# calculate inverse of convariance matrix')
self.classnum = int(max(self.targets))+1
fea_dim = len(self.trains[0])
trains_summed_by_class = [] # trainSummedByClass[0] -> train[targets==0]
self.mean_vec = [] # self.mean_vec[0] -> xp.mean(train[targets==0], axis=0)
for c in range(self.classnum):
trains_summed_by_class.append(self.trains[self.targets==c])
self.mean_vec.append(xp.mean(trains_summed_by_class[-1], axis=0))
self.convariance_matrixs = [] # cm[0] -> convariance_matrix of targets==0
self.inv_convariance_matrixs = [] # ここに各クラスごとの分散共分散行列の逆行列を入れる
for c in range(self.classnum):
convariance_matrix = []
for i in range(fea_dim):
convariance_vec = []
for j in range(fea_dim):
xi_mi = trains_summed_by_class.T[i] - self.mean_vec[i] # プログラムとしては転置は不要
xj_mj = trains_summed_by_class.T[j] - self.mean_vec[j] # 上記の式に合わせているだけ
convariance_vec.append( xp.sum( xi_mi * xj_mj, axis=0) / len(self.targets[self.targets==c]) )
convariance_matrix.append( convariance_vec )
self.convariance_matrixs.append( convariance_matrix )
convariance_matrix = xp.array(convariance_matrix, dtype=xp.float64)
print('# class {}, convariance_matrix has been created'.format(c))
inv_a = getInverse(convariance_matrix.copy())
self.inv_convariance_matrixs.append(inv_a)
逆行列を求めるgetInverseは以下になります。
numpyでは逆行列は2×2までしか取得できないので、自分で実装しています。
実装方法としては掃き出し法を愚直に書いています。
逆行列が無い(行列式=0)時は単位行列を返します。
(最終的にでてくる距離がユークリッド距離の2乗になるので今のままではマハラノビス距離との単純な比較には使用できないので注意してください)
def getInverse(matrix):
# unit mat
fea_dim = len(matrix)
inv_a = xp.array([[1.0 if i==j else 0.0 for i in range(fea_dim)] for j in range(fea_dim)], dtype=xp.float64)
if not xp.linalg.det(matrix)==0:
for i in range(fea_dim):
if matrix[i][i]==0:
for k in range(i, fea_dim):
if not matrix[k][i]==0:
tmp = matrix[k, :].copy()
matrix[k, :] = matrix[i, :].copy()
matrix[i, :] = tmp
tmp = inv_a[k, :].copy()
inv_a[k, :] = inv_a[i, :].copy()
inv_a[i, :] = tmp
break
buf = 1.0 / matrix[i][i]
inv_a[i, :] = inv_a[i, :] * buf
matrix[i, :] = matrix[i, :] * buf
for j in range(fea_dim):
if not i==j:
buf = matrix[j][i].copy()
inv_a[j,:] = inv_a[j,:] - inv_a[i,:] * buf
matrix[j,:] = matrix[j,:] - matrix[i,:] * buf
else:
print('det:', xp.linalg.det(matrix))
print(' so use unit matrix instead')
return inv_a
マハラノビス距離 を用いてクラスタリングしてみる
ページ上部にも貼りました以下の画像の黒い*点はどの属するでしょうか

実行してみます。
以下のコードでは実行毎にランダムに各クラスのデータのx,yとテストデータのx,yが決まります。
上の画像は以下のコードを実行した結果の一例です。
def main():
c1num = 100
xc1 = np.random.randn(c1num) * 10 + 70
yc1 = np.random.randn(c1num) * 15 + 40
c2num = 100
xc2 = np.random.randn(c2num) * 5 + 30
yc2 = np.random.randn(c2num) * 10 + 30
c3num = 100
xc3 = np.random.randn(c3num) * 3 + 40
yc3 = np.random.randn(c3num) * 7 + 70
xtest = np.random.rand(1) * 30 + 30
ytest = np.random.rand(1) * 30 + 30
trains = np.r_[np.array([xc1, yc1]).T, np.array([xc2, yc2]).T, np.array([xc3,yc3]).T]
targets = xp.r_[np.zeros(c1num), np.ones(c2num), np.ones(c3num)+1]
print('trains.shape:', trains.shape)
print('targets.shape:', targets.shape)
plt.plot(xc1, yc1, 'r.', label='class 0')
plt.plot(xc2, yc2, 'b.', label='class 1')
plt.plot(xc3, yc3, 'g.', label='class 2')
plt.plot(xtest, ytest, 'k*', label='class 4')
plt.xlim([0, 100])
plt.ylim([0, 100])
plt.savefig('test.png')
tests = np.array([xtest, ytest]).T
print('tests.shape:', tests.shape)
myMah = mahalanobis(trains, targets)
print('# mahalanobis distance')
print(myMah.pred(tests))
print('# euclidean distance')
# ユークリッド距離は実装してないのですが、Sを単位行列にして、結果を1/2乗して再現しています。
myMah.inv_convariance_matrixs[0] = xp.array([[1.0 if i==j else 0.0 for i in range(2)] for j in range(2)], dtype=xp.float64)
myMah.inv_convariance_matrixs[1] = xp.array([[1.0 if i==j else 0.0 for i in range(2)] for j in range(2)], dtype=xp.float64)
myMah.inv_convariance_matrixs[2] = xp.array([[1.0 if i==j else 0.0 for i in range(2)] for j in range(2)], dtype=xp.float64)
print(xp.sqrt(myMah.pred(tests)))
if __name__=='__main__':
main()
赤、青、緑の順に距離が出力されます。
> $ python mahalanobisML.py # use numpy trains.shape: (300, 2) targets.shape: (300,) tests.shape: (1, 2) # setup mahalanobis machine learning # calculate inverse of convariance matrix # class 0, convariance_matrix has been created # class 1, convariance_matrix has been created # class 2, convariance_matrix has been created # mahalanobis distance start prediction 100%|███████████████████████████████████████████████████████████████████| 1/1 [00:00<00:00, 4832.15it/s] [[ 6.6424745 22.5124097 17.82236989]] # euclidean distance start prediction 100%|██████████████████████████████████████████████████████████████████| 1/1 [00:00<00:00, 12826.62it/s] [[ 24.06498232 32.78967825 17.90650959]]
マハラノビス距離では赤が6.64で一番近く、次に緑の17.82です。
一方、ユークリッド距離では緑が17.90で一番近く、次に赤の24.06という結果になりました。
このようにユークリッド距離では平均のみを用いるので、場合によっては直感的に正しくない出力になります。
マハラノビス距離では分散を考慮しているので、平均値とは離れていても統計的にクラスタリング出来ることがわかります。
ということで、マハラノビス距離を用いた機械学習を実装してみたよ、でした。